|
2. Sequential seasonal adjustment.
A time series may be decomposed by calculating unseasonal average values of the terms and, alternatively, it may be decomposed by calculating unseasonal average change between terms. A moving average procedure typically concentrates on unseasonal average term-values, the arithmetic progression aims at deseasonalizing the average change between terms. To compare the methods, the moving average procedure was converted, in the preceding paragraph, from value-oriented to change-oriented and it was brought to light that unity ('constancy') of average unseasonal growth is inherently incompatible with the procedure. The following sequential adjustment procedure is change-oriented and adheres to unity of average growth between unseasonal quarter averages. This implies, that every addition to the series, being likely to change the average growth, also has an impact on the seasonal pattern. The arithmetic progression method opens the way to adjust the terms of a time series individually and in sequence (instead of in groups and retrospectively). This can only be done on the basis of the series' history and its current development, there is no hindsight of what happens afterwards. We shall first work out a procedure assuming that the seasonal components are stable or gradually evolving. The problem of aberrant values will be dealt with in paragraph 3. A sequential procedure includes three steps:
Step 1, forecast: Unseasonal quarter averages constitute an arithmetic progression; they can be seen as coordinates on a straight line through average value A, the 'average growth line'. Its gradient is the average quarterly growth g, its length is pj, where p is periodicity and j is the number of years of the inspected section of the series. The distance from the line's center, A, to the series' last term is (pj -1)/2. If the series is extended by one term, this term's distance from the original A is (pj-1)/2 + 1 = (pj + 1)/2 and the forecast for the adjusted value of the new term is A +{(pj + 1)/2}g = 14741 + {(4 x 7 +1)/2} x 99 = 16176 The new term's forecasted full value is found by adding the average seasonal component for quarters I, 16176 - 1321 = 14855 The extrapolation towards the current term can also be done by extending the agl : y 't = y 't-1 + g and then add the appropriate seasonal component. Step 2, Compare: The difference between the measured value and the expected value for 1996.I is 15631 - 14855= + 776. This difference will be called 'e' (for 'error'). In the unlikely case that e were zero, that is if the forecast for 1996.I would be spot on right, it could be concluded that
This combination would then be our best guess to adjust the new term. Step 3, Update growth and seasonal components: What if error e is not zero? The gradient of the average growth line and the subsequent average seasonal components cannot be applied to the individual new term, without leaving a rest value of which it is uncertain whether it is growth or season. As was noted at the end of paragraph 1, some doubt is thrown on the exclusive efficacy of gradient g. In Table 2 (paragraph 4) total growth measured by the full series varies widely over the same 6-years, depending on which corresponding periods are selected to measure the growth by. Between fourth quarters average growth (g) is 2396 / 24 = 99, but the second quarters would render a g of 1159 / 24 = 48! Average growth and season for the entire section of the time series appear to be rather randomly decided by the particulars of two extreme terms, implying that a whole range of other gradients may be equally valid. When updating growth and season in the light of a new addition to the series, a reasonable criterion to select a gradient g would be that it must exactly forecast the new term. Changing the gradient means revolving the average growth line around its fixed centre, swapping growth for season - or vice versa. The total value of unseasonal quarters remains as it was, the partition between seasonal and unseasonal components changes. The growth line that extends exactly to the new term has a gradient g, modified by dg in such a way, that {(pj + 1)/2}dg + change of seasonal component = e. |

|
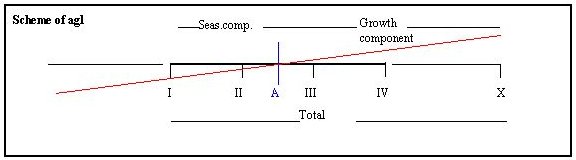
In the above scheme the bold line is the central section of the average growth line with gradient g, the four quarterly group averages are depicted at distances 1. The relevant quarter (I) is at A- (p-1)/2, that is A-1.5. The new term (X) is at position A + (pj+1)/2. The red line depicts the adjusted gradient, g + dg. At coordinates I through IV the vertical distances between the red line and the bold line represent the change of the seasonal components. We can now allot error e (+776) to the seasonal components and gradient g, applying the arithmetic progression of the change in agl gradient, dg. Sequential procedure versus centered moving average. In both procedures deseasonalized values can be derived for groups of corresponding quarters. The quarter averages of a centered moving average are:
The main difference between these procedures is the timing and scope of updating g. Updating g in a moving average procedure may be done at every new term (as in the sequential procedure), but it is more common to update at longer intervals. Then the updated seasonal corrections are applied in retrospect to all terms from the central term of the moving average onwards. In the sequential procedure only the current term is adjusted and this adjustment is considered to be final and the best guess in view of the series' history and its current development. |