|
3. How to deal with aberrant values.
A procedure is proposed to put sequential seasonal adjustment to practice. As an additional feature the procedure tries to recognize aberrant values instantly and regulate their impact on the set of seasonal corrections. The procedure includes
The parameters. As can be seen from the scheme of the agl, the impact of a change in gradient g depends on the distance of the new term X from the agl's center A. If the distance to X is larger, a smaller change of gradient g will bridge the gap e. Then the impact on the seasonal pattern will also be reduced. We can mitigate the impact of outliers on the seasonal pattern, by assuming a different length of the agl when outliers are met. What is needed, are criteria to decide whether a new term is an outlier or not, and parameters to set the assumed length of the agl accordingly. In the CAMPLET procedure five parameters are defined to set the length of the series in years (j) for every next term to be adjusted. CAMPLET is an acronym of the parameters:
The last two parameters, Limit to Error (LE) and Times (T) determine the particulars of every term in sequence. The criterion is forecasting error (e) as a percentage of the (absolute average of the last p terms of the) full series. Parameter LE decides whether a term is 'common' or aberrant. LE sets a limit, if (absolute) e exceeds this limit the term is dubbed as an aberrant value. Parameter T decides whether an aberrant value is an outlier or a break in the seasonal pattern. The criterion is the number of times the aberrant value returns consecutively in corresponding periods. Parameters Common Adjustment (CA), Multiplier (M) and Pattern (P) regulate the impact of the new term on the set of seasonal components. If the new term is not aberrant, parameter CA will set length j at a standard value. If the new value is an outlier parameter M will set j to a multiple of error e. If the new value is a break of pattern parameter P will set j to a low value (usually 1). Standard set up of parameters: 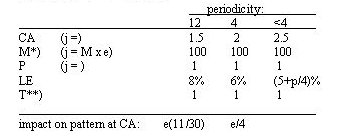
*) e is expressed in decimals. A constant value is subtracted to mitigate the multiplier for lower values of e, j = M x e - (LE - CA). For example: if e = 30% and p = 4, then
At the standard set up low values are selected for j by parameter CA, allowing what seems to be an overwrought impact on the seasonal pattern. But it must be kept in mind that the season is not updated by change along the average growth line, only by the deviations from this line. Moreover, the procedure is additive and, if the seasonal component varies proportional to the full series' level, a fair share of e must be allotted to the season to keep pace with the series' development. The impact of e on the pattern increases for lower values of j. In the standard set up a lower value for j is set for monthly series than for series with a lower periodicity. The reasoning for selecting these values is, that if periodicity is larger, growth per period will be smaller but seasonality is likely to increase. In the standard set up (T= 1) a break in the seasonal pattern will be recognized in the second year of its occurence and the new pattern will be adopted in that same year. Before that the new pattern will cause outliers that will enhance the volatility of the deseasonalized series. The shift of pattern will be depicted during T years in the deseasonalized series before it is adopted. ( Procedures that revise the seasonal pattern in retrospect will eventually adopt the new pattern at its first occurence, but it must be realized that such procedures may also anti date the new pattern, applying it on terms preceding the first occurence.) The standard set up will do for fairly stable series. If outliers are frequent, it is advised to raise LE considerably and/or lower M in order to allow some more impact of extreme values on season and gradient of the growth line. Then a stabilizing effect may be obtained by raising CA. Also frequent outliers may call for incrementing T, to avoid reshuffles of the seasonal pattern. The procedure. After the initial phase (see later) it takes five steps to adjust every new term: 1. Forecast the new term:
Initial phase: In the initial phase a provisional gradient g and a provisional set of seasonal components must be selected. One simple way to achieve this is to assume g = 0 for the first year of the series, and to select as seasonal components the differences of the p measured values minus the year's average value. Then for the terms of the second and third year apply the procedure, which will modify the set of seasonal components to something closer to reality. With this set of components the series can be adjusted, beginning at the first year all over again. In appendix B the quarterly series of sales of consumer durables is corrected by the CAMPLET procedure in its standard set up. |