|
4. Sequential outcomes or provisional outcomes.
Many sophisticated procedures have been developed to tune up the provisional outcomes of moving-average based procedures (see for example Makridakis c.s. on 'Forecasting'2). Some of these procedures distinguish evolutions in the seasonal pattern and extrapolate these to modify the average pattern in use. Such improved provisional adjustments must still be revised in retrospect when actual values are incorporated into a new moving average. A sequential procedure, by contrast, claims finality for its first results. These final results include a continuous evolution of the seasonal pattern , preluding a coming update of the pattern by moving average. In Appendix B the lower table states the applied seasonal adjustment for every single term of the time series. The pattern can be seen to shift continuously, particularly in 1992 and 1993 (the deviations from zero of the annual totals are an indication of the pattern's sweep). In no particular year and also not in the 7-years average of the pattern do we find the average seasonal pattern calculated by moving average or by the arithmetic progression procedure of paragraph 1 The differences between the seasonal pattern by CAMPLET and the pattern calculated by moving average indicate swaps between calculated growth and seasonal components. Compare the total 6-years growth (1995.IV - 1989.IV):
CAMPLET seems to have embezzled 2369 - 1905 = 464, or almost 20%, of growth! The missing growth is hidden in the fourth quarter seasonal component: CAMPLET seasonal component 1995.IV - 1989.IV: 3367 - 2903 = 464. While the static average seasonal component of a moving average does not meddle with growth between corresponding periods, CAMPLET does so very much: Table 2: 6 years growth (1989-1995) between corresponding periods: 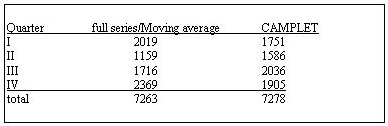
The growth over the same stretch of time, but measured between the disparate corresponding periods, varies strongly both in the moving average and in the CAMPLET adjustment. To some extent unseasonal fluctuations will be responsible for this. But also the growth between the same quarters as measured by each of the procedures is quite different and these differences equal the changes of the CAMPLET seasonal pattern. I like to think that these differences represent residual seasonal fractions disguised as growth in the unupdated moving average. These differences constitute what I see as the advantage in time of CAMPLET over a moving average. See also appendix C for a comparison between Camplet and Census x-11 Arima. It has been pointed out to me, that seasonality is more of a stable factor than one that shifts up or down at every new term. But I fail to see the basic difference between updating a pattern at longer intervals or updating it all the time. A preference for a more static pattern is, I think, more based on habit than on reasoning. Seasonality, as I see it, consists of fluctuations that are typical for corresponding periods of a time series. If a term is added to a series, one could see the extended series as an entirely new one, of which the typicalities may be interpreted in the light of the recent addition. 1 Barend Abeln owns a bureau for economic analysis of interim company data in Bussum, the Netherlands. email babeln@worldonline.nl 2 Spyros Makridakis, Steven C. Wheelwright and Victor E. McGee. Forecasting: methods and applications. Second edition, 1983, John Wiley & Sons. |